Test du temps limite VMA en natation

Test du temps limite VMA en natation

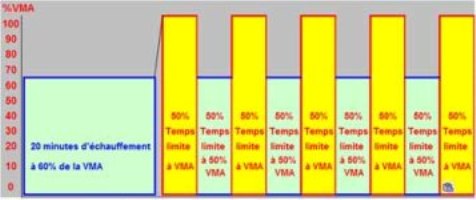
Il y a quelque temps, j’ai lu le livre très intéressant de Véronique Billat intitulé « Physiologie et méthodologie de l’entraînement de la théorie à la pratique ». À l’intérieur de ce livre, pages 139 et 160, elle nous explique qu’après étude, il a était montré que des coureurs sont capables de soutenir 5 répétitions à vVO2max (plus petite vitesse qui sollicite le volume d’oxygène maximal) d’une durée égale à 50% du temps limite à vVO2max. Les temps de récupération sont courus à 50% de vVO2max et sont égaux aux temps des fractions courues à 100% de vVO2max.

Après lecture

Ceci m’a beaucoup intéressé, puisque désormais il est peut-être possible d’évaluer le temps total de travail à vVO2max en fonction du nombre de répétitions que l’on souhaite faire.

On peut retranscrire cette affirmation par cette équation :

tpsW_total = nbr * ( ß * tpsLim_vVO2max)

 avec :

tpsW_total = Temps total de travail
nbr = Le nombre de répétitions
ß = Facteur du temps limite à vVO2max
tpsLim_vVO2max = Le temps limite à vVO2max

Prenons un exemple concret avec un athlète qui a réalisé un test pour déterminer sa vVO2max (17km/h) et un autre test pour connaître son temps limite à cette vitesse (4 minutes).

tpsW_total = 5 * ( 0,5 * 4 )

On peut donc dire que cet athlète peut réaliser une séance d’entraînement constituée de 5 répétitions de 2 minutes courues à 17km/h, soit un temps total de travail de 10 minutes. C’est le principe même de « l’intervalle training« . On fractionne une distance ou un temps pour finalement en faire plus que si on devait parcourir une seule fois une longue distance ou une seule fois un temps limite. En temps normal, cet athlète ne peut courir que 4 minutes à 17km/h, mais en divisant le temps limite par 2, il pourra courir 5 fois 2 minutes à 17km/h soit un total de 10 minutes !  Avec ce type d’entraînement, Véronique Billat a relevé des progressions allant jusqu’à 1,2km/h de vVO2max au bout de 4 semaines sur des athlètes ayant déjà une bonne vVO2max.

5*(2′ à 17km/h récup=2′ à entre 8,5 et 10,2 km/h)

Hypothèses

 Cela a immédiatement suscité beaucoup d’interrogations chez moi dont voici les trois principales :

1. Si je souhaite faire plus de 5 répétitions, quel sera le coefficient de réduction du temps limite ?
2. Quelles sont les limites haute et basse du temps de travail total ?
3. Peut-on appliquer cette équation pour d’autres sports comme la natation ?

Ces questions sont importantes, car la monotonie d’un entraînement est source de désentraînement. Il est donc important de varier les répétitions, les temps de repos et les intensités pour maintenir le côté ludique des séances. De même, il serait intéressant de voir si on peut appliquer cette équation pour tous les sports dans lesquels on peut pratiquer l’intervalle training.

Nombre de répétitions et coefficient de réduction

J’ai donc d’abord tenté de répondre à ma première question de la façon suivante :

Lors d’un test de temps limite, on réalise bien un seul exercice pour déterminer le temps limite. On a donc « 1 » répétition pour « 1 » temps limite. On obtient ainsi un temps total de travail qui correspond au temps limite à vVO2max.

tpsW_total = 1 * ( 1 * tlim_vVO2max ) = tlim_vVO2max

Et nous savons que pour réaliser 5 répétitions à 100% de vVO2max, il faut réduire de moitié le temps limite.

tpsW_total = 5 * ( 0,5 * tlim_vVO2max) = 2,5 * tlim_vVO2max

Comment passer de l’une à l’autre. Est-ce arithmétique ou géométrique ? Un moyen très simple permettra de savoir si l’une ou l’autre des méthodes est meilleure, à savoir que le principe même de l’intervalle training est d’augmenter le temps de travail total à l’allure cible.

Méthode arithmétique

Est-ce que pour passer de 1 à 5 répétitions on doit ajouter « +5 » ? Pour le coefficient de réduction, la réponse est plus évidente, à savoir qu’il faut diviser par 2 et non retirer « -0,5 ». Posons donc quelques étapes suivantes et vérifions si le temps de travail augmente. Si c’est le cas, on pourra la comparer avec la suivante…

• tpsW_total = 1 * ( 1 * tlim_vVO2max ) = tlim_vVO2max
• tpsW_total = 5 * ( 0,5 * tlim_vVO2max) = 2,5 * tlim_vVO2max
• tpsW_total = 10 * ( 0,25 * tlim_vVO2max) = 2,5 * tlim_vVO2max
• tpsW_total = 15 * ( 0,125 * tlimvVO2max) = 1,875 * tlim_vVO2max

Inutile de continuer, on voit bien que le temps total n’augmente pas. Celui-ci diminue même si on souhaite faire 15 répétitions.

Méthode géométrique

Passons à la méthode géométrique où ici on multiplie par 5 les répétitions et on divise toujours par 2 le coefficient de réduction.

• tpsW_total = 1 * ( 1 * tlim_vVO2max ) = tlim_vVO2max
• tpsW_total = 5 * ( 0,5 * tlim_vVO2max) = 2,5 * tlim_vVO2max
• tpsW_total = 25 * ( 0,25 * tlim_vVO2max) = 6,25 * tlim_vVO2max
• tpsW_total = 125 * ( 0,125 * tlim_vVO2max) = 15,625 * tlim_vVO2max
  …

Cette méthode semble donc plus intéressante et elle permet même de se dire qu’Émil Zatopek était vraiment en avance sur son temps. En effet, il était adepte de l’intervalle training et faisait parfois jusqu’à 100 répétions de 400m avec 200m de récupération. Toutefois il semblerait qu’il ne courait pas à 100% de vVO2max mais à 90%.

Limite basse et haute du temps total de travail

Maintenant que nous avons une méthode, calculons les limites. La plus facile est la limite basse avec :

tpsW_total = 1 * ( 1 * tlim_vVO2max ) = tlim_vVO2max

Pour déterminer la limite haute, je fixe la limite du temps de répétition à 30 secondes. Ce type de séance est bien connu. Le fameux 30/30 pour travailler sa VO2max. Il faut désormais trouver un moyen pour que le coefficient de réduction du temps limite donne au minimum 30 secondes.

Je vous passe les détails des calculs. Ils ne sont pas primordiaux pour la suite de cet article, de plus je me suis arrangé pour vous donner un exemple plus parlant pour ne pas que vous décrochiez ainsi que ma correctrice bien aimée (trop trad).

Pour que tout cela soit plus explicite, reprenons l’exemple de notre athlète avec un temps limite de 4 minutes (soit 240 secondes). Eh bien devinez quoi : 0,125*240 ça donne 30 ! C’est pas beau ça ?!

Donc, théoriquement, cet athlète pourrait réaliser une séance course à pied contenant 125 répétitions de 30 secondes courues à 17km/h avec des récupérations de 30 secondes également ! Avec une telle séance, il effectuerait 62’30 » de travail. Nous venons de trouver la limite haute.

Mise en application

Vous êtes sans doute quelque peu surpris de la limite haute du temps total de travail possible. Par conséquent, pour répondre à ma troisième question, il me semble évident que je devais tester cette équation sur le terrain. Rassurez-vous, je n’ai pas demandé à l’un de mes athlètes de réaliser cela pour moi. Je me suis personnellement investi dans cette tâche mais pas sur les 125 répétitions, je me suis contenté des 5. L’expérience est simple, si, sur une séance où je dois réaliser 5 répétitions à vVO2max je craque avant ou si je suis en mesure d’en faire 6, alors cela veut dire que c’est défaillant.

J’ai réalisé ce test en natation. Dans cette discipline, j’ai une vVO2max de 4.011km/h est un temps limite de 5’59 » (soit 359″). Avec ces données, ma série test se compose ainsi => 6 * ( 200m en 2’59″50 r=45″). Je ne récupère que 45″ car en natation les temps sont plus courts qu’en course à pied. Ci-dessous vous trouverez le détail de la séance.

Comme vous pouvez le voir, j’ai volontairement choisi de faire 6 répétitions et non 5 comme le spécifie l’équation. Cela permet justement de tester la validité de celle-ci. J’étais dans une piscine avec un couloir pour moi tout seul, dans une eau à 29°C et je n’ai effectué aucun apport en glucide durant toute la séance.

Voici le détail de mes temps de passages :

1. 200m en 2’56″09 =>176,09″
2. 200m en 3’00″44 => 180,44″
3. 200m en 2’59″44 => 179,44″
4. 200m en 2’58″94 => 178,94″
5. 200m en 2’59″29 => 179,29″
6. 200m en 3’00″16 => 180,16″

Un peu de statistiques

De tout évidence l’équation ne fonctionne pas pour la natation. J’ai toutefois réalisé quelques calculs de statistiques pour confirmer les résultats de ce test.

Valeur(s) aberrante(s)

Lorsque l’on regarde mes temps on remarque que mon premier 200m est trop rapide. Est-ce que ce chrono mérite que l’on en tienne compte dans la suite des calculs ? La méthode de Dixon permet de calculer cela. Je classe d’abord mes chronos par ordre croissant :

176,09 ; 178,94 ; 179,29 ; 179,44 ; 180,16 ; 180,44

r10=(178,94-176,09)/(180,44-176,09)=0,655

Je compare ce résultat avec la valeur critique qui est de 0,56 pour α=5 et n=6 et on constate que 0,655 est supérieur à 0,56, mon premier chrono est donc considéré comme aberrant. Par conséquent, il n’entrera pas dans la suite de mes calculs.

Moyenne

On peut désormais connaitre la moyenne de mes temps de passages qui est de : 179,654″ soit 2’59″654. Cela montre que je n’ai pas nagé assez vite en moyenne de 154 centièmes (mais je pense que c’est négligeable).

Variance

Puis passons à la variance de ces données validées. Je vous passe là aussi les calculs, le résultat est : 0,312384 secondes².

Écart-type

L’écart-type est donc d’environ : 0,559 secondes. Mes chronos sont donc pertinents s’ils sont compris entre 179,095″ et 180,213″. Cela représente donc 3 bons chronos sur 5 soit 60%. Si on compte mon loupé du début cela fait 3 bons chronos sur 6.

Conclusion

Après tout cela, il semblerait que je sois obligé de refaire le test en essayant d’être plus régulier. Cela laisse également transparaître le fait qu’en natation on puisse faire, non pas 5 mais 6 répétitions à 0,5*tpsLim. Mais avant de tirer des conclusions trop hâtives, il serait intéressant d’effectuer d’autres tests et pourquoi pas, si vous souhaitez m’aider, n’hésitez pas à m’envoyer vos propres tests de terrain afin de combiner nos expériences et ainsi affiner nos connaissances.